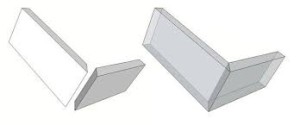
In the last post we looked at creating a four sided box that could be used as a bucket or planter box. The idea is to build a wooden cask or barrel by eventually increasing the number of sides or staves required to help the cask stay together and hold water without using glue. We build two versions. The first has straight sides and creates a 4x4x4 cube. The second is a little more complex and creates the same cube but reduces the bottom of the cube to 3 inches.
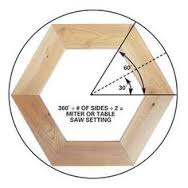
What would it take to make a six sided box of the same design? If we go to our on-line angle calculator we see that we need to cut the angle at 30 degrees rather than 45 degrees. The big question becomes how wide each side or stave should be.
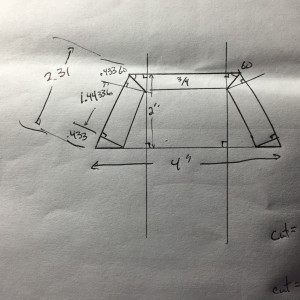
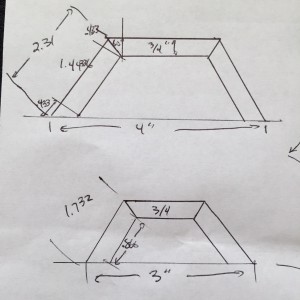
We want the entire piece to fit into a 4 inch square so we need to use geometry to calculate the length of each board. Two things that we know from the design are that three of these sides need to fit into four inches. This gives us The total width of the three sides combined. We also know that the total height of the three sides combined needs to fit into two inches. From this we can calculate the length of each board.
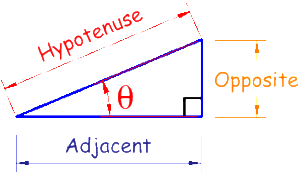
There are a few things to note. First the middle piece is parallel to the centerline. From this we can create a right triangle from the inside edge cut. We know that the thickness of the wood is 3/4 of an inch so we know one side of the triangle. We also know the angle of the resulting cut to be 60 degrees because we move the 30 degree part with the table saw. Using an online geometry assistant we can calculate the length of the wood remaining from the cut. If we draw a straight line at 90 degrees to the centerline we know the angle is 30 degrees and the height of the triangle is two inches. From this we know the angle and adjacent and want to calculate the hypotenuse.
We can calculate the Hypotenuse with one of the following equations:
|
SOH…
|
Sine: sin(θ) = Opposite / Hypotenuse
|
|
…CAH…
|
Cosine: cos(θ) = Adjacent / Hypotenuse
|
|
…TOA
|
Tangent: tan(θ) = Opposite / Adjacent
|
H = A / cos(angle). We know that A is 2 inches and the angle is 30 degrees. It is important to realize that Excel uses radians so the outer length of the wood (hypotenuse) = A / cos (angle / 180 * pi()) = 2 / cos(30/180*pi()) = 2.3094. This is perfect because we can use this to cut the width of our board. We need to cut it 4 inches high with a 90 degree cut. We then reset the table saw blade to 30 degrees and cut one edge then set the blade guide to make the second cut 2.31 inches wide. The outer edge to outer edge will be 2.31 inches long. The inner edge will be (2 – 3/4) / cos(30/180*pi()) or 1.443 inches.
The next exercise is to build the tapered bucket where the top is four inches and the bottom is three inches.
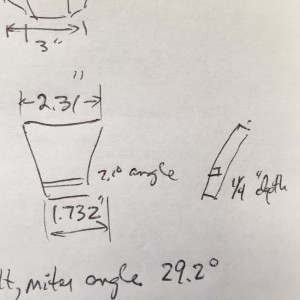
The angle that we used for the four sided box translates here as well. The top of the box ends up being 2.31 inches. The bottom of the box can be calculated by using the 1.5 inch centerline with a 3/4 inch thick wood at a 30 degree angle. This calculates out the width of the bottom of the taper to be 1.732 inches. Using the on-line calculator the blade tilt should be 29.7 degrees. This results in a cut of six pieces that should fit together.
The resulting physical boxes look like
Note that we use blue painters tape to hold the pieces together. We are close to being a round so a metal band might or might not hold the box together. We are getting close. Next up, an eight sided box is the next project. We might need to increase the size of the box because the width of each board is getting a little small when you try to cut it with a table saw. We will probably try to fit this into a 8 inch square because it basically just doubles all of the measurements.